day4-深度优先搜索DFS
1. 剑指 Offer 12. 矩阵中的路径

要点:
- 第一步确定是回溯算法,其实就是暴力解锁,一个个尝试,个人认为回溯算法有两类问题:一是找一个解,二是找所有解。像这题就是找一个解,找到了就可以结束,若是要求找所有正确路径,那就是第二类问题。两类问题区别在于返回值,单解问题遇到失败情况后撤销上一步选择回到上一步状态后同时返回一个失败标志,上一步利用此标志进行判断是否继续尝试;若遇到成功情况则直接返回成功标志,上一级判断为标志为成功后也返回一个成功标志,逐级退出程序,停止尝试。而所有解问题在遇到失败情况后撤销上一步选择回到上一步状态,继续尝试;若遇到成功情况则进行记录,然后返回到上一步状态继续尝试其他可能,直至遍历完所有可能性。
- 这道题有一个需要注意的地方是第一个值的候选列表和后面所有值的候选列表是不一样的,第一个值的候选列表是矩阵中所有元素,所以要行列循环,后面值的候选列表是周边的值,因此需要两部分要分开写代码,主函数里的两个循环是第一个的选择,backtrack函数里面是后面值的选择。
- 回溯算法核心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
成功路径列表
路径
def backtrack_one():
if 失败:return False
if 成功:return True
# 1.对当前节点进行操作,记录值或改变状态等等(先序操作)
for 选择 in 选择列表:
# 做选择
路径.append(选择)
if backtrack_one():return True
# 退出选择,
# 2.对当前节点进行操作,记录值或改变状态等等(中序操作)
路径.pop()
# 3.对当前节点进行操作,记录值或改变状态等等(后序操作)
return False
def backtrack_all():
if 失败:return
if 成功:成功路径列表.append(路径)
for 选择 in 选择列表:
# 做选择
路径.append(选择)
backtrack_all()
# 退出选择,回到上一状态
路径.pop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
def backtrack(i,j,k):
if i<0 or i==m or j<0 or j==n or board[i][j] != word[k]:return False
if k == l-1:return True
board[i][j]=''
flag = backtrack(i-1,j,k+1) or backtrack(i+1,j,k+1) or backtrack(i,j-1,k+1) or backtrack(i,j+1,k+1)
board[i][j]=word[k]
return flag
if not board or not word:return False
m,n,l = len(board),len(board[0]),len(word)
for i in range(m):
for j in range(n):
if backtrack(i,j,0):return True
return False
另外加了一个记录路径的功能
1 | class Solution: |
记录所有可能的路径
1 | class Solution: |
DFS 和 二叉树的三种遍历方法有什么关系?
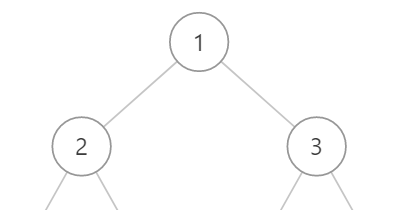
- DFS一般是多叉树,每个节点的子节点不一定有几,一般做选择前用
for 选择 in 选择列表:,二叉树,显然是其中一个特例而已,只有左右两个孩子,for循环没必要,直接写两次选择就好。 - DFS个走到1之后,会继续向下走到2,走不下去之后返回1,再走向3,走不下去再返回1,最后回到1的父节点,这个过程中有三个时机可以看到1,在z这三个时机处理1分别对应先序遍历、中序遍历和后序遍历
2. 剑指 Offer 13. 机器人的运动范围
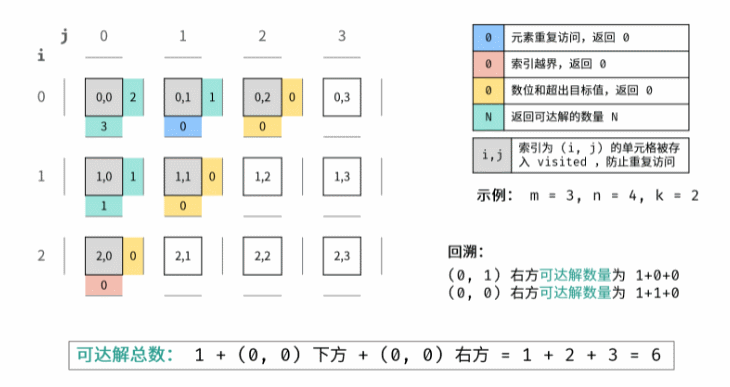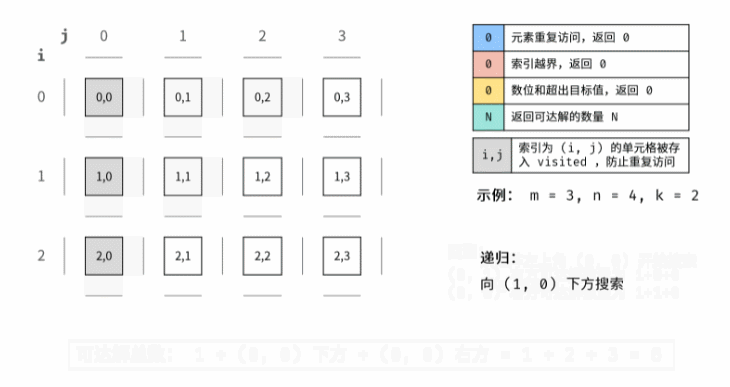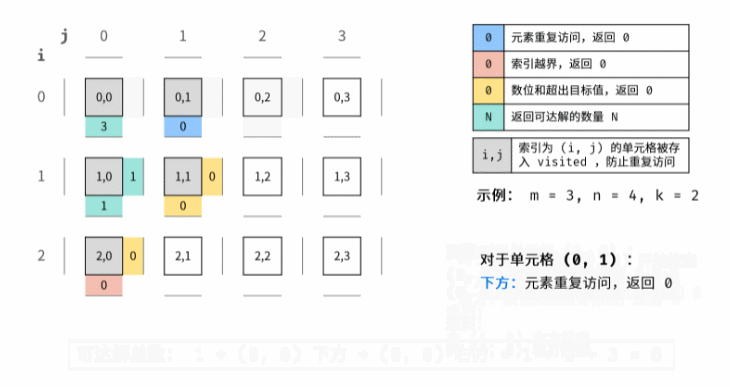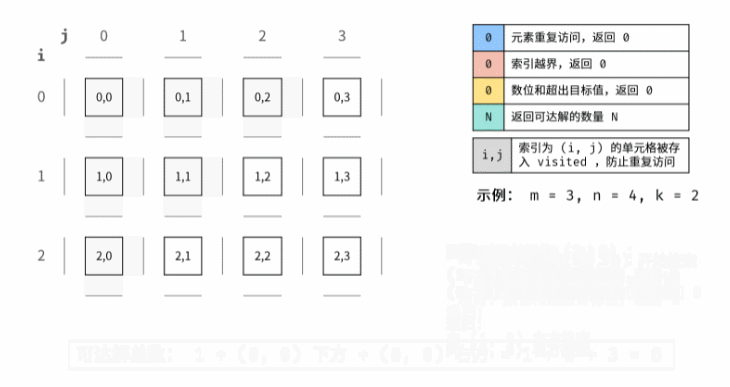
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution:
def movingCount(self, m: int, n: int, k: int) -> int:
def numSum(x):
sum=0
while x:
s = x%10
x = x//10
sum+=s
return sum
visited = []
def trackback(x,y):
if x>=m or y>=n or numSum(x)+numSum(y)>k or (x,y) in visited:return 0
visited.add((x,y))
return 1+trackback(x+1,y)+trackback(x,y+1)
visited = set()
return trackback(0,0)
3. 剑指 Offer 27. 二叉树的镜像
1 | # Definition for a binary tree node. |
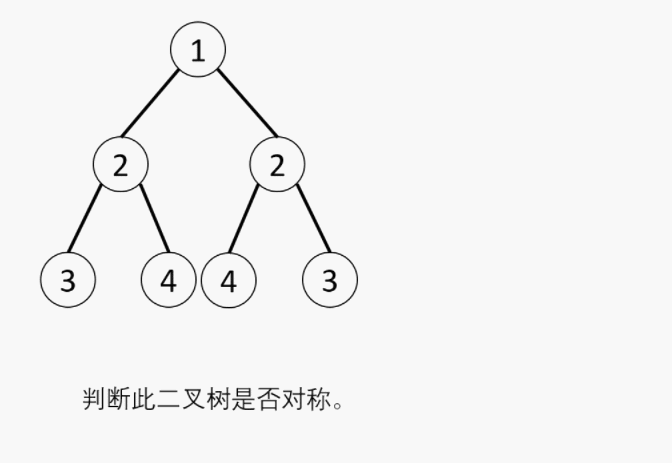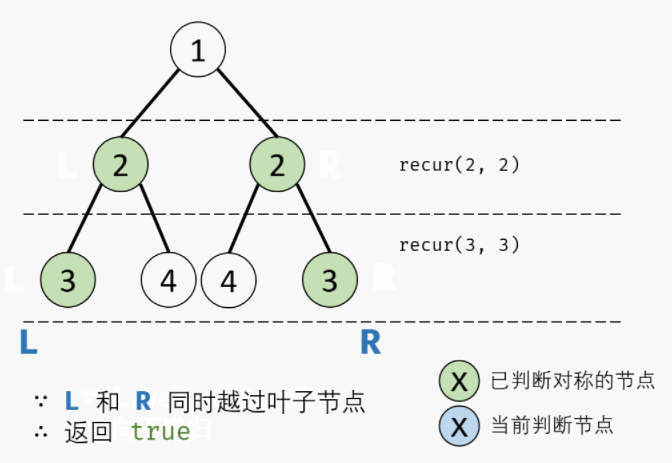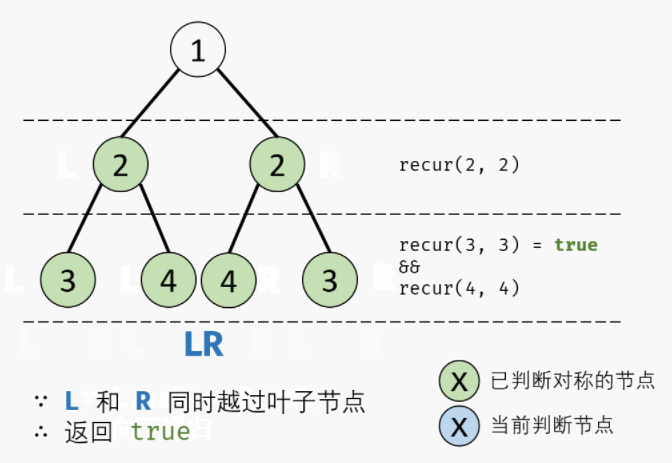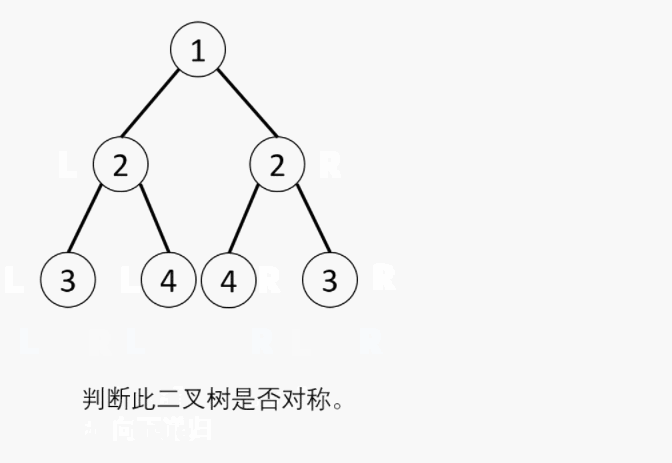
4. 剑指 Offer 28. 对称的二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
def dfs(L,R):
if not L and not R:return True
if not L or not R or L.val != R.val:return False
return dfs(L.left,R.right) and dfs(L.right,R.left)
return True if not root else dfs(root.left,root.right)
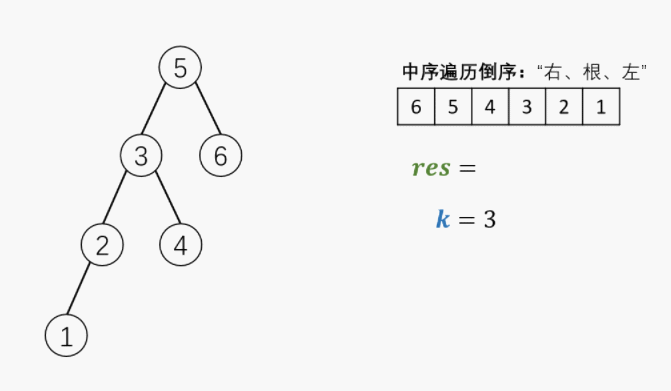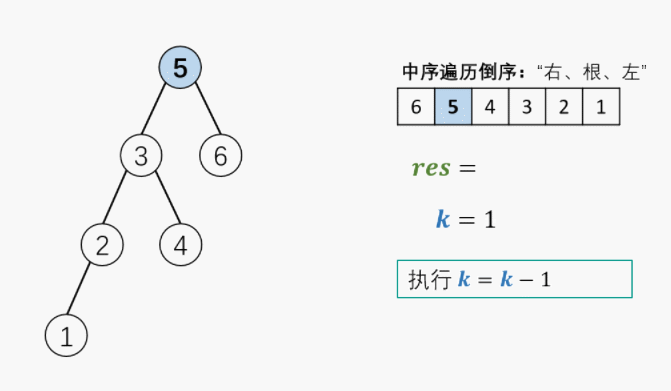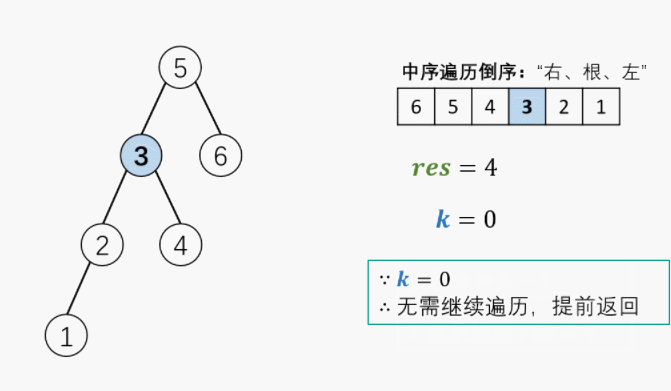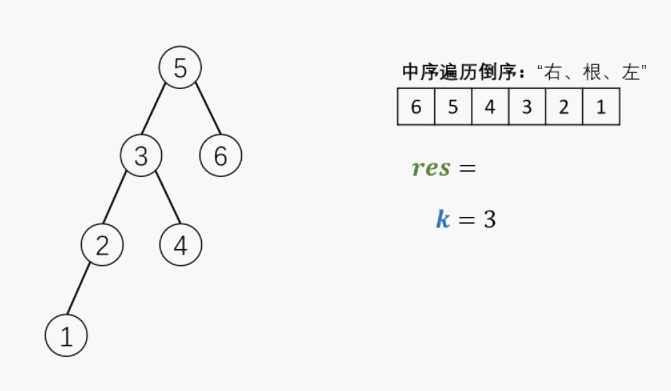
5. 剑指 Offer 54. 二叉搜索树的第k大节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def kthLargest(self, root: TreeNode, k: int) -> int:
def dfs(root):
if not root:return False
if dfs(root.right):return True
self.rank+=1
if self.rank==k:
self.num = root.val
return True
if dfs(root.left):return True
self.rank = 0
self.num = -1
dfs(root)
return self.num
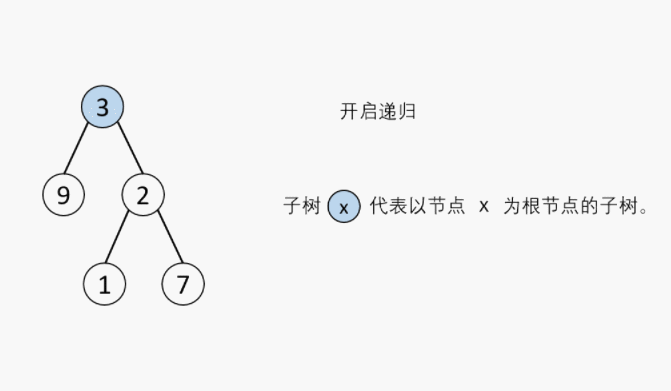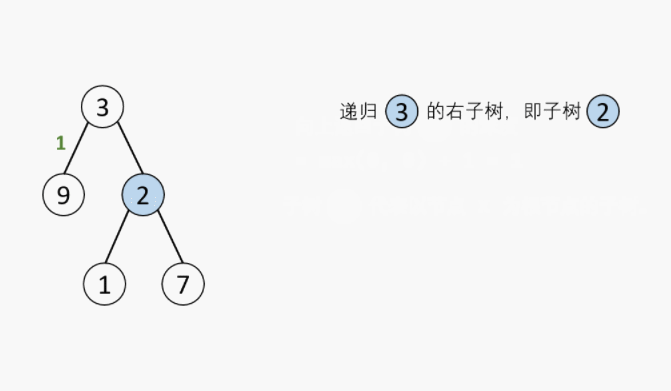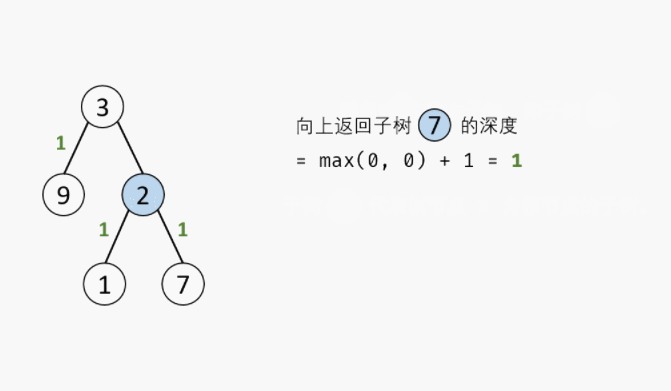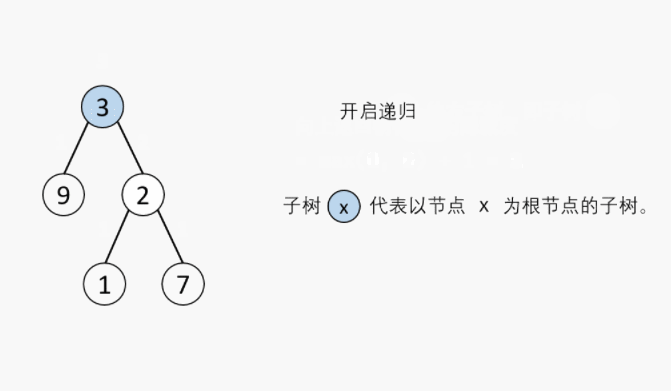
6. 剑指 Offer 55 - I. 二叉树的深度
1
2
3
4
5
6
7
8
9
10
11
12# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:return 0
return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
