1. 信息熵、交叉熵、相对熵

详细解释

信息熵

  • 代表随机变量X或整个系统的不确定性。
  • 熵越大，随机变量或系统的不确定性就越大。
  • 也是要消除这个不确定性所要付出的最小努力。
  • 公式：，其中的也叫做自信息

交叉熵

  • 用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
  • 这个值越小说明该非真实分布越接近真实分布。
  • 这也是为什么在机器学习中的分类算法中，我们总是最小化交叉熵，因为交叉熵越低，就证明由算法所产生的策略最接近最优策略，也间接证明我们算法所算出的非真实分布越接近真实分布。
  • 公式：

相对熵

  • 也称KL散度，用来衡量两个取值为正的函数或概率分布之间的差异。
  • 相对熵 = 某个策略的交叉熵 - 信息熵（根据系统真实分布计算而得的信息熵，为最优策略）。
  • 可以将第一个分布看做真实分布，第二个分布看做非真实分布。
  • 公式：

2. sigmoid和softmax

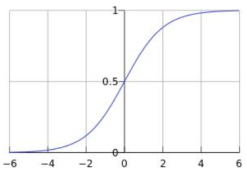
sigmoid

  • sigmoid将一个(负无穷，正无穷)上的数映射到一个(0，1)上的数

softmax

  • softmax将n个(负无穷，正无穷)上的数映射到n个(0，1)上的数,且这n个数之和为1

关联

  • sigmoid可以看成是softmax的一个特例，即另一个通道固定是常数0

3. 逻辑回归

二分类

样本数据：$\left\{\left(\mathbf{x}^{( i) },y^{( i) }\right)\right\}_{i=1}^{m}$，$\mathbf{x}^{( i) } \in \mathbb{R}^{n}$ ，$y^{( i) } \in\{0,1\}$，$m$为样本数量
hypothesis函数：$h_{\theta}(\mathbf{x})=\sigma\left(\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n}\right)$
待定参数：$\theta=\left(\theta_{0}, \theta_{1}, \cdots, \theta_{n}\right)^{\top}$
引入$x_{0}=1$，$\mathbf{x}=\left(x_{0}, x_{1}, x_{2},\cdots, x_{n}\right)^{\top}$
简化$h_{\theta}$，得

使用交叉熵作为损失函数，使用交叉熵时想清楚三个问题，随机变量是什么？真实分布是什么？预测分布是什么？
随机变量是输出的类别，也就是y
真实分布对每个样本来说都不一样，可以看到对每个样本来说都是0-1分布，$
P\{y=k\}=p^{k}(1-p)^{(1-k)}
$，$k$有两种取值，0或1，$p$代表1的概率。当某个样本类别为1时，$p=1$;当某个样本类别为0时，$p=0$
预测分布$P\{y=1\}=h_{\theta}(\mathbf{x})$，$P\{y=0\}=1-h_{\theta}(\mathbf{x})$

y=0 y=1
$q(y)$ $1-h_{\theta}(\mathbf{x})$ $h_{\theta}(\mathbf{x})$
类别为1时 $p(y)$ 0 1
类别为0时 $p(y)$ 1 0
类别为1时 $p(y)\log\frac{1}{q(y)}$ 0 $\log\frac{1}{h_{\theta}(\mathbf{x})}$
类别为0时 $p(y)\log\frac{1}{q(y)}$ $\log\frac{1}{1-h_{\theta}(\mathbf{x})}$ 0

根据交叉熵公式求每个样本的交叉熵$\operatorname{cost}\left(\mathbf{x}^{( i) }, y^{( i) }\right)$

改写成整体表达时：$\operatorname{cost}\left(\mathrm{x}^{( i) }, y^{( i) }\right)=-y^{( i) } \cdot \log \left(h_{\theta}\left(\mathrm{x}^{( i) }\right)\right)-\left(1-y^{( i) }\right) \cdot \log \left(1-h_{\theta}\left(\mathrm{x}^{( i) }\right)\right) .$
所有样本的整体损失函数：

梯度下降更新参数：

下面主要推导怎么得到$\left(h_{\theta}(x^{( i)})-y^{( i)}\right) x_{j}^{( i)}$
以一个样本i为例：

先算出：

代入：

多分类